Unele din cele mai fascinante construcții din matematică, nu doar prin complexitatea, dar și prin frumusețea modelelor pe care le generează, sunt fractalii. Pe lângă multitudinea de aplicații pe care aceștia le au în domenii tehnice, ei sunt o provocare pentru înțelegerea noțiunilor de dimensiune în matematică. Intuim deseori ce înseamnă ca o figură să fie unidimensională, bidimensională sau tridimensională, dar ce poate oare însemna o dimensiune de 0.631 sau 1.2619? Mai mult, putem vedea cum diferite metode de a defini dimensiunea (mărimea, măsura) unui obiect pot genera rezultate atât de opuse precum 0 și infinit, în cazul aceluiași fractal.
Marea majoritate a fractalilor sunt construiți cu așa-numita proprietate de autosimilaritate, în sensul că figura este formată din copii identice ale figurii inițiale. Această proprietate o vom valorifica pentru a da o a cincea intuiție teologică, după cele din articolele [4] și [5].
Mulțimea Cantor
Vom vorbi pentru început despre o construcție celebră, cu implicații interesante atât în domeniul matematicii, cât și sub aspectul ideilor (filozofice) pe care le poate genera. Construcția a fost realizată prima dată de către matematicianul german Georg Cantor și reprezintă unul dintre cele mai simple exemple de mulțime autosimilară sau fractal.
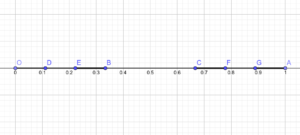
Construcția începe prin considerarea unui segment de dreaptă, pe care, pentru simplitate, îl vom presupune a avea capete 0 și 1. În continuare, împărțim acest segment în trei părți, urmând a elimina porțiunea din mijloc. În Figura 1 de mai jos, e prezentată mulțimea după două iterații. Mai întâi, se elimină segmentul BC, apoi segmentele DE și FG. Lungimea porțiunii rămase este egală cu 4/9, adică (2/3)2.
Procedeul continuă în același mod: eliminăm porțiunile din mijloc ale fiecărui segment din figură. La fiecare pas, lungimea totală a mulțimii rezultate este două treimi din lungimea de la pasul anterior și, prin urmare, după un număr de n pași, lungimea totală va fi egală cu (2/3)n. Cu cât facem mai mulți pași, această lungime va fi din ce în ce mai mică, apropiindu-se oricât de mult de 0.
Numim mulțimea Cantor (notată K) rezultatul aplicării procedeului de mai sus de o infinitate de ori. Prin urmare, lungimea totală a mulțimii K este 0, deoarece trebuie să fie mai mică decât lungimea de la orice pas intermediar, aceasta din urmă devenind oricât de mică, pe măsură ce aplicăm pașii algoritmului.
Paradoxal însă, deși lungimea totală este 0, rămânem cu o infinitate de elemente în urma eliminărilor succesive. Mai mult, elementele mulțimii K sunt tot atât de multe cât cele din întreg intervalul inițial [0,1]. Argumentul pentru această afirmație se bazează pe scrierea numerelor în bazele de numerație 2 și 3, demonstrația fiind redată mai jos în anexă.
În continuare, vom prezenta o a treia metodă de definire a dimensiunii unor astfel de figuri, metoda care determină titulatura de fractal a mulțimii K. Mai întâi, însă, trebuie să înțelegem ce reprezintă conceptul de autosimilaritate (engl. self-similarity). Privind din nou Figura 1, observăm că am fi putut aplica algoritmul plecând de la segmentul OB, obținând o copie mai mică a mulțimii K. Segmentul OB nu are nimic special în acest sens, copii mai mici ale mulțimii K se pot obține aplicând algoritmul pentru orice segment component de la orice pas al construcției. Prin urmare, mulțimea K este aceeași (doar contractată) în fiecare parte componentă, fiind numită autosimilară.
În legătură cu această proprietate, putem defini conceptul de dimensiune Hausdorff–Besicovitch (noțiune mai generală, dar ușor de definit în contextul figurilor autosimilare, a se vedea [1]), concept ce caracterizează (într-o anumită măsură) ceea ce uzual numim obiecte unidimensionale, bidimensionale și tridimensionale, în maniera ce o vom descrie în paragraful următor.
Să considerăm un pătrat în plan și o copie de 3 ori mai mică a acestuia (Figura 2). Numărul necesar de pătrate mici care să acopere pătratul mare este 9=32. Puterea 2 care apare dă dimensiunea Hausdorff–Besicovitch a pătratului. Evident, puteam contracta figura de 4 sau 5 ori, spre exemplu, obținând acoperiri cu 16=42 sau 25=52 pătrățele, puterea 2 fiind independentă de coeficientul de contractare.
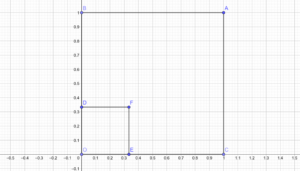
Pentru mulțimile autosimilare cum este K putem aplica aceeași procedură. Observăm că segmentul OB se obține prin contractarea de 3 ori a segmentului inițial OA, deci copia mulțimii K aferentă segmentului OB este contracția de 3 ori a mulțimii K. Similar, copia aferentă segmentului CA este tot o contracție de 3 ori a mulțimii K, iar cele două copii acoperă toată mulțimea Cantor K. Prin urmare, avem nevoie de două copii la scară 1:3 ale lui K pentru a acoperi toată mulțimea K. Formula de mai sus ne spune că dimensiunea Hausdorff–Besicovitch d a mulțimii K satisface relația 3d=2. Acest număr d este notat log32 și este egal aproximativ cu 0.631. Prin urmare, dimensiunea Hausdorff–Besicovitch a mulțimii K nu este un număr întreg, este o fracție zecimală (infinită), de unde denumirea de fractal.
Fulgul de zăpadă al lui Koch
Următorul exemplu de fractal a fost pus în evidență în 1904 de matematicianul suedez Helge von Koch. Figura e construită în plan, după următoarea regulă: se consideră triunghiul echilateral ABC iar fiecare latură se împarte în trei segmente. Pornind de la segmentele din mijlocul celor trei laturi, se construiesc în exterior alte trei triunghiuri echilaterale, apoi procedura se continuă cu fiecare segment obținut pe conturul exterior (Figura 3). După aplicarea de o infinitate de ori a algoritmului, obținem o figură plană asemănătoare unui fulg de zăpadă (Figura 4).
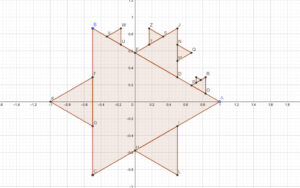
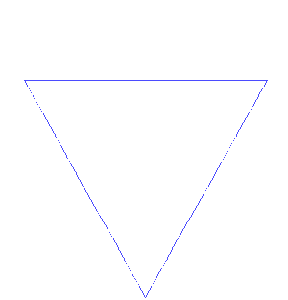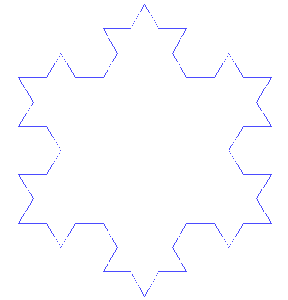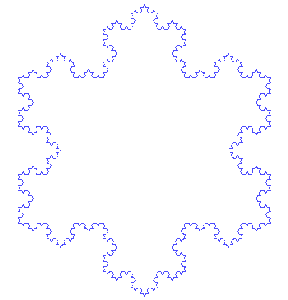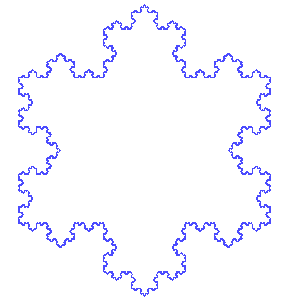
Faptul că se aplică o infinitate de pași ne scutește de a avea segmente mici „neprocesate” (pentru care împărțirea și construcția triunghiului central nu au avut loc), care ar strica autosimilaritatea.
Putem aplica același procedeu ca în cazul mulțimii Cantor pentru a determina dimensiunea Hausdorff–Besicovitch a porțiunii autosimilare a fulgului de zăpadă cu baza pe AB. Astfel, dacă ne uităm la construcțiile obținute din aplicarea algoritmului (de o infinitate de ori, desigur) pentru segmentele BE, EJ, JD și DA, ele vor fi patru copii contractate la scară 1:3 a figurii inițiale. Prin urmare, formula 3d=4 (unde 3 este coeficientul de contracție și 4 este numărul de copii necesare pentru a acoperi porținuea din figură cu baza pe AB) ne conduce la a afirma că dimensiunea căutată este log34, aproximativ 1.2619.
Remarcăm că în fiecare din cele două cazuri considerate, dimensiunea Hausdorff–Besicovitch s-a dovedit a fi mai mică decât dimensiunea spațiului ambiant: dreapta (unidimensională) și planul (bidimensional).
Alte proprietăți interesante (a se consulta [2] pentru detalii) ale Fulgului de zăpadă Koch sunt faptul că acesta are arie finită și perimetru infinit. Pentru mai multe exemple de fractali, împreună cu dimensiunile Hausdorff–Besicovitch aferente, se poate consulta resursa [3].
A cincea intuiție teologică
În finalul articolului, voi încerca să sugerez o legătură între conceptul de autosimilaritate și o noțiune teologică. În acest scop, voi da o altă modalitate în care putem formula proprietatea de autosimilaritate a fractalilor: Mulțimea se găsește întreagă în oricare parte a ei. Acest fapt mă duce cu gândul la considerațiile dogmatice cu privire la Trupul Euharistic al Lui Iisus Hristos, despre care se afirmă:
Se frânge și Se împarte Mielul lui Dumnezeu, Cel ce Se sfărâmă și nu Se desparte, Cel ce se mănâncă pururea și niciodată nu Se sfârșește (…) [6]
Chiar dacă în această formulare nu este atât de evidentă intuiția legată de autosimilaritate, explicația din [7] a Părintelui Profesor Dumitru Stăniloae este grăitoare:
După prefacerea elementelor, Domnul este prezent în Euharistie, întreg, nu numai sub fiecare din cele două chipuri ale pâinii și vinului, ci și în fiecare părticică din ele. [7, pag. 69]
Învățătura că întregul Hristos este în Euharistie și pretutindenea, că Trupul și Sângele Domnului sunt neîmpărțite, iar împărțirea și pluralitatea privește chipurile pâinii și vinului este statornic afirmată de Sfânta Tradiție. Patriarhul Eutihie al Constantinopolului (în Cuvânt despre Paști) spune : «Se primește întreg Sfântul Trup și Sânge al Domnului, chiar dacă se primește numai o parte din acelea (pâine și vin); căci se împarte neîmpărțit în toate pentru amestec». [7, pag. 71]
Hristos încă înainte de împărțirea chipurilor este prezent întreg în fiecare parte a lor, fără ca să fie mai mulți Hristoși, cum e sufletul în toate părțile trupului. [7, pag. 71]
Concluzie
Acestea fiind spuse, observăm pluralitatea noțiunii de dimensiune, măsură, dată de faptul că un spațiu aproape gol (i.e. mulțimea Cantor) poate adăposti o infinitate de obiecte. Doar modul de măsurare este cel care face distincția între mare și mic, deși toate cele trei modalități de evaluare a mărimii sunt la fel de valide intuitiv în cazuri simple. Aceeași diferență de viziune o regăsim și la Fulgul de zăpadă Koch, unde un perimetru infinit adăpostește o arie finită. Este Fulgul de zăpadă infinit sau nu? Este mulțimea Cantor infinită sau nulă? Poate infinitul să fie nul? Răspunsul este: depinde cum privim lucrurile.
Pe un alt plan, noțiunea de autosimilaritate și cea de dimensiune fracționară reprezintă o dovadă în plus a faptului că nu tot ceea ce pare la prima vedere ilogic este necesar fals, aici încadrându-se inclusiv conceptele teologice greu de perceput.
Anexă (mai tehnică)
Prezentăm în continuare schița demonstrației faptului că mulțimea K și intervalul [0,1] au același număr de elemente. Pentru cititorul nefamiliarizat cu noțiunea de număr cardinal, recomandăm citirea primei părți a articolului [4] înainte de parcurgerea demonstrației ce urmează.
Numerele din intervalul [0,1) se pot scrie sub formă de numere „cu virgulă” în modul uzual în baza 10 – scriere zecimală – dar și în alte baze (ne interesează 2 – scriere binară – și 3 – scriere ternară) după cum urmează:
Numărul 0,5 în baza zece (uzuală) reprezintă o jumătate, adică fracția 1/2. De fapt, scrierea zecimală 0,5 codifică faptul că ne referim la 5 părți din 10, adică o jumătate sau, cu alte cuvinte, o parte din două. Scrierea în baza 2 a acestui număr este astfel 0,1 (o parte din două – prin analogie cu 5 părți din 10, cifra de după virgulă arătând câte părți din cantitatea cuantificată de bază avem).
Mai departe, numărul 0,25 reprezintă 25 de părți din 100=102, adică o pătrime, o parte din 4=22. Prin urmare, scrierea în baza 2 a acestui număr este 0,01 (01 părți din 22). Un ultim exemplu este cel al lui 0,11 în baza 2, ce poate fi exprimat ca suma dintre 0,1 și 0,01 (binare). De mai sus, suma aceasta în scriere zecimală este 0,5+0,25=0,75 (trei sferturi).
Remarcăm că în scrierea binară (în baza 2) avem doar cifre de 0 și 1. Prin analogie, putem defini scrierea în baza 3, folosind cifrele 1 și 2. Să luăm spre exemplu numărul 0,12 în baza 3. Acesta este suma între 0,1 și 0,02 (ternare), ce se traduce prin 0,3=o parte din trei + 0,02=două părți din nouă. În final, numărul 0,12 ternar codifică 5 părți din 9 (nu uităm că o parte din 3 este același lucru cu 3 părți din 9, deci, în total, avem 3 părți din 9 plus două părți din nouă). În formă zecimală, vom avea scrierea 0,5555555… cu o infinitate de cifre de 5 (doar împărțiți 5 la 9 pe orice calculator de buzunar pentru a vedea rezultatul).
Mai rămâne doar să observăm faptul că numerele excluse la construcția lui K sunt exact cele care nu conțin cifra 1 în scrierea ternară. Spre exemplu, primul interval eliminat [1/3,2/3] conține numere ce au prima cifră 1 după virgulă în baza 3. Numerele din intervalele eliminate DE și FG (Figura 1) au cea de-a doua cifră egală cu 1. În final, mulțimea K va avea doar numere scrise cu cifrele 0 și 2 în baza 3.
Cu aceste informații în minte, putem construi corespondența bijectivă dintre mulțimea Cantor și intervalul [0,1].
Pentru fiecare număr din K, înlocuim cifra 2 din scrierea în baza 3 cu cifra 1 și considerăm rezultatul în baza 2. Spre exemplu, numărul ternar 0,2002=2/3+2/(34) va fi asociat cu 0,1001=1/2+1/(24) binar. Din cele de mai sus, deducem că această corespondență este bijectivă, deci mulțimile au același număr de elemente.
NOTE
[1] Shailesh A Shirali, „Fractal Dimension and the Cantor Set, Resonance”, Journal of Science Education, Vol. 19, Issue 11, Indian Academy of Sciences, Noiembrie 2014, pp. 1000-1004.
[2] https://en.wikipedia.org/wiki/Koch_snowflake (accesat la 14 iulie 2021).
[3] https://en.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension (accesat la 14 iulie 2021)
[4] https://www.syntopic.ro/cateva-intuitii-matematice-pentru-notiuni-teologice-partea-i/.
[5] https://www.syntopic.ro/cateva-intuitii-matematice-pentru-notiuni-teologice-partea-a-ii-a/.
[6] Sfânta Liturghie a Sf. Ioan Gură de Aur, Liturghier, EIBMBOR, București, 2012.
[7] Pr. Prof. Dumitru Stăniloae, „Dumnezeiasca Euharistie în cele trei confesiuni”, în Ortodoxia, nr. 1/1953, pp. 46-115.
Imagine copertă: Created by Wolfgang Beyer with the program Ultra Fractal 3. – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=32197.

