În informatică și în matematica aplicată, termenul de euristică desemnează, la modul general, un pas sau o strategie de rezolvare a unei probleme caracterizată de pragmatism, aleasă în defavoarea unei abordări analitice ce s-ar putea dovedi prea dificilă sau chiar imposibil de aplicat în anumite condiții date. Euristicile sunt scurtături, de multe ori spectaculoase, pe drumul de la problemă la soluție, care adesea sacrifică anumite calități ale rezultatelor, precum precizia sau completitudinea, în favoarea unui timp de calcul mult îmbunătățit.
O strategie euristică poate fi întrebuințată, de pildă, la găsirea soluțiilor unui sistem de ecuații ce implică dificultăți majore (cum ar fi un sistem de ecuații neliniare), dar și la găsirea în timp rezonabil a unui drum între două noduri dintr-un graf (de exemplu, între două localități pe o hartă). Nu în ultimul rând, rețelele neuronale moderne, ce stau la baza răsunătoarelor reușite reunite sub denumirea generică (și pe alocuri exagerată) de inteligență artificială, sunt, de fapt, sisteme antrenate în manieră euristică1 – o încrucișare neliniară de parametri interni ce sunt ajustați printr-un procedeu repetitiv și totodată prudent, din aproape în aproape, pentru ca, în cele din urmă, acest procedeu să realizeze un sistem capabil să efectueze cu precizie rezonabilă felurite predicții cu privire la datele de intrare – de pildă, să recunoască semne tipografice, chipuri umane sau obiecte extrase dintr-o fotografie.
Dezvoltarea strategiilor euristice este remarcabilă nu numai pentru rezultatele pe care acestea le furnizează, ci și pentru că, nu de puține ori, principiile pe care se întemeiază sunt metafore schematizate ale unor procese ample întâlnite în natura înconjurătoare. Un exemplu emblematic în acest sens îl reprezintă clasa de algoritmi denumiți generic algoritmi evolutivi2, ce modelează simplist dar uluitor de eficient procesele evolutive ale populațiilor speciilor din natură, utilizându-le, de această dată, pentru a rezolva probleme inginerești dificile. În speranța de a stârni fascinația și aprecierea cititorului tehnic și non-tehnic deopotrivă, vom urmări în continuare un exemplu concret al desfășurării unui astfel de algoritm.
Să presupunem situația în care, ca parte dintr-un proiect ingineresc, intenționăm să găsim soluția următorului sistem de ecuații, respectiv valorile necunoscutelor x, y și z din mulțimea numerelor reale pentru care toate cele trei ecuații ce urmează sunt adevărate:
\[
\left\{
\begin{array}{ll}
x^2-9 = 0\\
\sqrt{x-2} + 2yz = 0\\
y \cdot \sin y + y^2 – 3=0
\end{array}
\right.\]
Pentru acest sistem de ecuații neliniare, o rezolvare analitică este fezabilă (deși nu chiar trivială) și furnizează rezultatele \( x = 3 \), \(y \approx -2,1797 \), \(z \approx 0,2293 \). În practică, însă, realizarea automată a raționamentelor analitice este un proces relativ anevoios chiar și folosind un program software, mai ales când forma ecuațiilor este necunoscută a priori. Pentru a ieși din acest impas și pentru a determina o soluție pentru acest sistem fără a fi nevoiți să lucrăm cu „forma” (funcțiile) ce intră în componența acestuia, chiar fără să avem pretenția nici măcar să cunoaștem sistemul apriori, vom dezvolta în cele ce urmează următoarea strategie:
Ne vom imagina cele trei numere căutate \((x, y, z) \) drept codificarea trăsăturilor („ADN-ul”) unor ființe dintr-o specie imaginară, al căror scop este să supraviețuiască și să se reproducă într-un mediu înconjurător mai degrabă ostil. Putem privi cele trei numere drept „genele ADN-ului” iar punerea laolaltă a genelor o vom numi, convenabil, cromozom3 – așadar, vom studia indivizi definiți de un cod genetic (cromozom) cu trei gene.4
Mediul înconjurător ostil va fi generat de problema pe care vrem să o rezolvăm, în cazul nostru – sistemul de ecuații neliniare. Cerința ca valorile să rezolve toate cele trei ecuații în același timp este deosebit de constrângătoare – există o singură combinație de numere care îndeplinește perfect aceste condiții, iar aceasta conține oricum numere iraționale (care nu vor putea fi exprimate niciodată exact, având un număr infinit de zecimale nerepetitive). Nu vom găsi soluția exactă, însă ne vom mulțumi cu una pe care o vom considera suficient de apropiată de cea exactă.
Asumându-ne în continuare un ingrat dar necesar rol de Demiurg – din fericire doar virtual –, vom demara algoritmul propriu-zis prin definirea mai multor soluții-candidat la rezolvarea sistemului, respectiv indivizi ale căror gene (numere) inițiale le vom alege aleatoriu – aceștia vor constitui populația inițială. Numărul indivizilor populației îl vom fixa la exact 500.
În continuare, vom evalua cât de adecvat este fiecare individ pentru mediul său, în funcție de bagajul genetic propriu – altfel spus, cât de capabil este să facă față „adversității” de a rezolva toate cele trei ecuații concomitent, de unde vom încerca să cuantificăm cât de îndreptățit este fiecare individ să supraviețuiască și să se înmulțească. În algoritmul nostru, acestei judecăți a adecvării care se petrece în natură îi corespunde calculul unei funcții de evaluare care „dă o notă” fiecărui membru al populației curente. Pentru exemplul dat, am conceput o funcție de evaluare care furnizează o „notă” între 0 și 105, în funcție de cât de mult aceste valori apropie rezultatul expresiilor din sistemul de ecuații de valoarea urmărită 0, atunci când înlocuim necunoscutele cu valorile indivizilor.
Spre exemplu, individul
\( (x, y, z) = (2,7996; -0,0870; -8,3119) \) va primi „nota” \(6,29\), deoarece înlocuind valorile în sistemul de ecuații, vom găsi că expresiile produc valorile \((-1,1622; 2,34; 2,6257)\), însă individul
\( (x, y, z) = (2,9912; -1,6909; 0,3131) \) va primi „nota” \(9,68\) conform aceleiași formule, producând rezultatele \( (-0,0527; 0,0632; 0,3075) \) – numere subunitare mult mai apropiate de rezultatele ideale \((0, 0, 0)\).
În funcție de scorul de adecvare calculat, fiecare dintre cei 500 de indivizi va avea șanse proporționale să își reproducă propriile gene în viitoarea generație, grație unui proces similar selecției naturale. Reproducerea poate avea loc fie prin „clonarea” propriilor gene pentru a produce un nou individ identic, fie prin combinarea (încrucișarea) genelor a doi indivizi „părinți” pentru a produce „copii” care să-i înlocuiască. În cazul nostru, încrucișarea ar putea însemna, de pildă, interschimbarea unor gene între doi părinți, în speranța că se vor obține indivizi mai adaptați. Spre exemplu, din părinții \( (2,9508, -1,1971; 0,4791) \) și \((3,0067, -1,7576; 0,2441)\), am putea obține copiii \( (2.9508, -1,7576; 0,2441)\) și \( (3,0067, -1,1971; 0,4791) \).
În natură, momentul reproducerii este uneori succedat de încă un eveniment de importanță crucială, ancorat puternic în hazard – mutația, ce presupune alterarea aleatorie (sau cel puțin inexplicabilă) a unor gene, ducând la dezvoltarea unor trăsături complet noi. Acest eveniment poate fi atât benefic cât și dăunător pentru individ și este unul dintre mijloacele prin care are loc adaptarea incrementală la mediu, deoarece un individ pentru care ajustarea primită este benefică va fi favorizat, pe cale de consecință, să supraviețuiască și să-și multiplice genele. Și acest proces își găsește corespondentul în strategia noastră, fiind următorul pas în dezvoltarea populației de indivizi. În cazul nostru, mutația va însemna ajustarea în plus sau în minus cu o valoare foarte mică aleasă aleatoriu (mai mică decât 0,5) a valorilor genelor unui număr de indivizi selectați și ei tot aleatoriu, în speranța că măcar o parte dintre noii indivizi „mutanți” se vor dovedi mai bine adaptați, apropiindu-se de soluția problemei.
Recapitulând, după generarea candidaților inițiali, am efectuat: evaluarea lor, selecția celor mai adaptați, încrucișarea și mutația lor. Acești pași au descris ciclul de viață al primei generații de soluții-candidat. Desigur, noua generație de 500 de indivizi va prezenta schimbări față de cea precedentă, însă acestea vor fi, cel mai probabil, mici, dacă nu chiar neglijabile. La fel ca în natură, deviațiile semnificative ale trăsăturilor tipice ale populațiilor au loc de-a lungul unui număr mare de generații, așa încât și noi vom simula acest aspect, repetând ciclul evaluare-selecție-încrucișare-mutație de un număr mare de ori, de ordinul zecilor de mii. Vom observa că, pe măsură ce generațiile se succed, soluțiile noastre primesc, în general, „note” din ce în ce mai bune, ceea ce înseamnă că obținem soluții din ce în ce mai acceptabile, respectiv, indivizii sunt din ce în ce mai adaptați. Ne mai rămâne doar să oprim „timpul virtual” atunci când observăm că generațiile ulterioare nu mai produc schimbări importante și să extragem, din generația finală, cel mai performant candidat, considerându-l drept soluția căutată.
Pentru a exemplifica cele prezentate până acum, am realizat și o implementare proprie a acestui algoritm, ale cărui rezultate le vom urmări în continuare. În următorul tabel, putem observa evoluția valorilor corespunzătoare celui mai performant individ din generația sa, cât și a scorului de adecvare a acestuia, după un anumit număr de iterații ale algoritmului.
| Numărul generației | x | y | z | Scor |
| 1 (populația inițială) | 2,7996 | -0,0870 | -8,3119 | 6,295 |
| 10000 | 2,9508 | -1,1971 | 0,4791 | 9,110 |
| 20000 | 2,9912 | -1,6909 | 0,3131 | 9,682 |
| 30000 | 3,0067 | -1,7576 | 0,2441 | 9,694 |
| 40000 | 3,0004 | -1,8713 | 0,2431 | 9,804 |
| 50000 | 2,9971 | -2,0041 | 0,2346 | 9,895 |
| 60000 | 2,9971 | -2,0570 | 0,2432 | 9,941 |
| 70000 | 2,9967 | -2,0368 | 0,2410 | 9,929 |
| 80000 | 3,0000 | -2,0792 | 0,2358 | 9,949 |
| 90000 | 3,0003 | -2,1805 | 0,2296 | 9,998 |
Observăm că după a 90000-a iterație, valorile obținute sunt deja foarte apropiate de cele calculate analitic (3; -2,17976; 0,2293), așadar, putem concluziona că strategia noastră a funcționat.
Pentru o și mai bună vizualizare a fenomenului, iată și o serie de reprezentări grafice ale valorilor x și y ale poziției soluțiilor-candidat în raport cu soluția determinată analitic după un anumit număr de generații al unei alte simulări produse de aceeași implementare. În graficele ce urmează, punctele albastre reprezintă soluții-candidat (indivizi) din populația unei anumite generații în simularea noastră, iar punctul roșu reprezintă soluția determinată analitic către care țintim6.
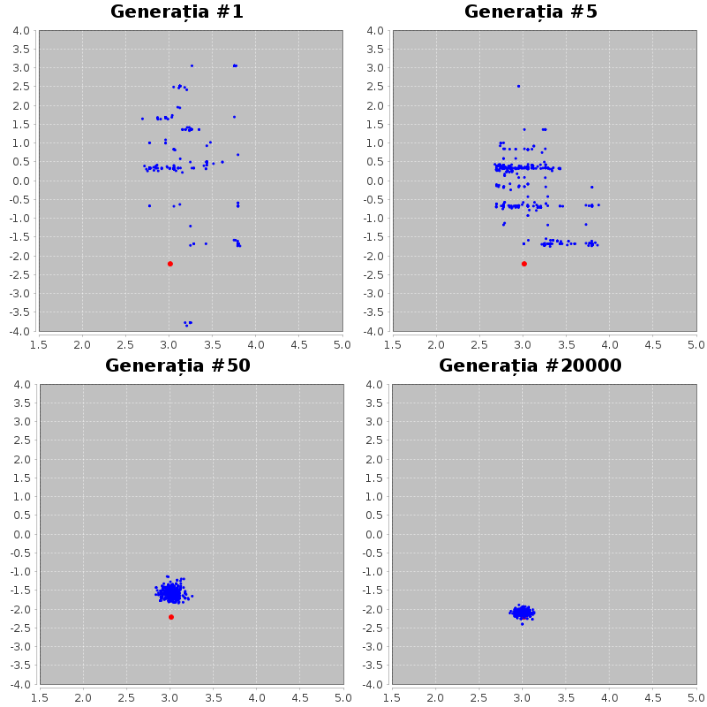
În aceste imagini, concentrarea graduală a indivizilor populației în jurul punctului „cel mai confortabil” este și mai evidentă. În cea mai înaintată generație reprezentată, soluțiile-candidat prezintă în continuare aberații față de soluția reală, însă cele mai bune soluții-candidat sunt deja atât de apropiate de cea reală încât acoperă reprezentarea acesteia în desen – acesta fiind un semn că simularea își atinge scopul.
Ceea ce am prezentat anterior este un exemplu concret al unui algoritm evolutiv, o așa-numită metaeuristică – o euristică de nivel înalt ce presupune un șablon în care sunt inserate alte euristici mai mici –,7 care imită procesul evolutiv din natură așa cum a fost descris pentru prima oară în mod faimos de Charles Darwin în secolul XIX.
Iar algoritmii evolutivi, descriși pentru prima dată în 19648, nu sunt nicidecum singurele metaeuristici inspirate din natură. Metoda denumită Particle Swarm Optimization9 dezvoltată în 1995, pornește de la maniera de deplasare în grup a vietăților, cum ar fi un stol de păsări aflat în zbor sau un banc de pești, pentru a obține soluții la probleme de optimizare, simulând totodată aspecte a ceea ce se numește „inteligența de roi” (en.: swarm intelligence). Și mai recent, în anul 2015, un nou algoritm metaeuristic inspirat din natură, denumit Ant Lion Optimizer10 a obținut rezultate foarte bune prin imitarea strategiei de vânătoare a larvelor de leul-furnicilor, o insectă ale cărei larve își capturează prada săpând în nisip gropi în formă de pâlnie, pe care le ajustează incremental, în funcție de productivitatea fiecăreia.
Performanțele obținute de acești algoritmi nu sunt mereu înțelese, ele fiind subiect de dezbatere între specialiști, însă reușitele lor sunt deja asumate conjectural, după ce au fost probate experimental în nenumărate instanțe. Astăzi, atât calculul evolutiv cât și clasa mai cuprinzătoare a metaeuristicilor sunt parte integrantă a materiei de studiu a facultăților de profil, fiind încadrate, de regulă, sub disciplinele care abordează domeniul Inteligenței Artificiale.
Succesul aplicării în planul abstract al matematicii al acestor principii schițate de om prin observarea naturii reprezintă un indiciu puternic cu privire la corectitudinea și gradul de obiectivitate al acestora, sau cel puțin un indiciu că, în marea euristică a cercetării științifice la care trudește întreaga omenire, aceste descoperiri se apropie semnificativ de mult de înțelegerea obiectivă a unor fenomene fundamentale ce guvernează universul. Performanța algoritmilor evolutivi este, așadar, un argument greu de tăgăduit în favoarea fenomenului evoluției și o sursă bogată de fascinație pentru ingineri, încapsulată într-o miniatură ușor replicabilă a acestei subtile, dar esențiale, minuni a naturii.
Note
- Dumitrescu, D., „Algoritmi genetici și strategii evolutive – aplicații în Inteligența artificială și în domenii conexe”, Editura Albastră, Cluj-Napoca, 2006, p. 35. ↑
- Ibidem, p. 34. ↑
- În acest caz particular, termenul „cromozom” nu realizează o paralelă foarte precisă, deoarece, în natură codul genetic al organismelor este compus, de regulă, din mai mulți cromozomi. În această prezetare, am menținut terminologia din literatura de specialitate. ↑
- Având în vedere numărul uriaș de gene al codului genetic al organismelor vii, un cromozom format din doar trei gene ar putea părea, la prima vedere, un instrument exagerat de simplu, însă în acest, caz complexitatea derivă din mulțimea posibilităților de alegere a celor trei numere, care este infinită – mulțimea numerelor reale. În cazul ADN‑ului/ARN‑ului, complexitatea apare ca urmare a numărului genelor. Există și o altă variantă de algoritmi evolutivi mai apropiată morfologic de corespondentul din natură, ce folosește cromozomi de lungime mai mare ce utilizează o codificare binară discretă (0/1), respectiv așa-numiții algoritmi genetici, cf. Dumitrescu. ↑
- În implementarea mea am ales drept funcție de evaluare expresia min(0,max(10, 10-||x||2)) unde ||x||2 este norma euclidiană a vectorului care reprezintă soluția-candidat („individul”). ↑
- Pentru simplitate, am păstrat în aceste reprezentări doar valorile x și y ale soluțiilor, omițând valoarea z pentru a evita necesitatea realizării unor reprezentări în spațiu tridimensional greu de interpretat vizual pe un suport static. ↑
- Algoritmii evolutivi presupun detalii de implementare precum coeficienți de probabilitate pentru operațiunile de selecție, încrucișare și mutație, strategiile propriu-zise de selecție, încrucișare, etc., precum și alte alegeri strategice făcute de proiectantul algoritmului pentru sporirea performanței acestuia. Pentru simplitatea prezentării, am omis menționarea acestora în paragrafele anterioare. ↑
- Fogel, L. J., Owens, A. J. and Walsh, M. J., „An evolutionary prediction technique”, International Conference on Microcircuit Theory and Information Theory, Tokio, Japonia, 1964, pp. 173–174. IEEE Press. ↑
- J. Kennedy and R. Eberhart, „Particle swarm optimization”, Proceedings of ICNN’95 – International Conference on Neural Networks, Perth, WA, Australia, 1995, pp. 1942-1948 vol.4, doi: 10.1109/ICNN.1995.488968. ↑
- Mirjalili, S., „The Ant Lion Optimizer”, Advances in Engineering Software, 2015, pp. 80-98, vol. 83. ↑
Imagine: Unsplash

